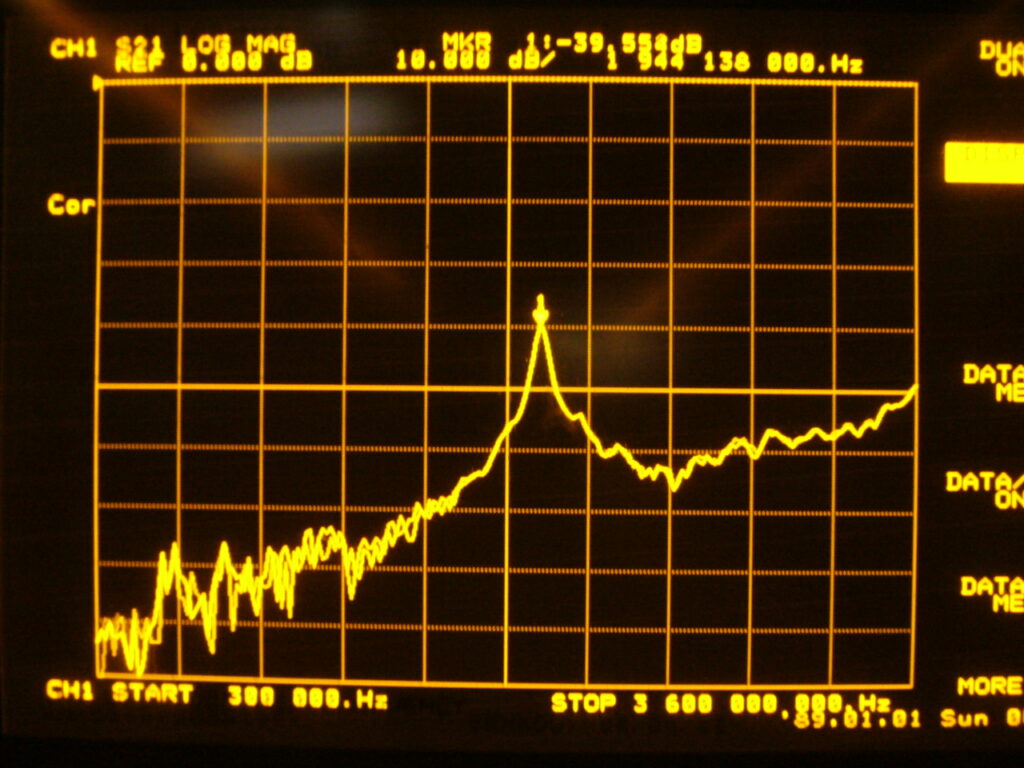
シールドされていない,グランド板が小さい場合の実験結果はシミュレーションとも理論とも大幅に食い違うおそれがあります.そのような現象をシミュレーションで再現するしようとすると非常に長い時間がかかって,しかも実験より乏しい知見しか得られないおそれがあります.この記事では非常に単純で現象のメカニズムのわかりやすい事例を紹介します.
前書き
“シミュレーションの結果は測定と一致しますか?” これはシミュレータを使うにあたってもっとも重要な問題です. しかし、私は(多分同業他社のかたがたも)この質問に対して 明確に答えることができません.
一見シンプルですが 非常に厳密な解析あるいは実験が必要な例題を紹介します. この問題ではほとんどの方が シミュレーションの結果と測定を一致させられない でしょう. 原因はグランド電位が不安定なことです. この文書の中では、 その原因について解説し、シミュレーションで再現します.
測定前の考察
ここで取り上げる例を実際に作りました.

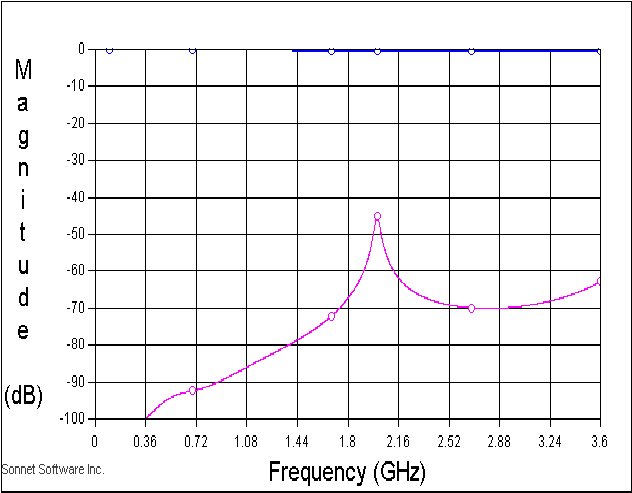
1.6mmのガラエポ基板の上に50Ωのマイクロストリップ線路を作ってあります. 基板の裏側はべたアースで、SMAコネクタを半田付けしてあります. マイクロストリップ線路は、途中2箇所で切断されています. 切断された間隔は基板の厚さと同程度で、直列キャパシタとして働きます. 二箇所の切断箇所の間隔は約40mmで、これは2GHzの1/2波長です. 1/2波長の線路は直列共振回路と等価ですから、 結果的にこのサンプルは直列共振回路を小容量で接続した形になり、 その周波数特性は、周波数が上がるに従って通過が多くなり、2GHzで極大となる であろうことが想像できます.

測定
側壁のあるサンプル
測定結果は考察どおりで、 安定している.

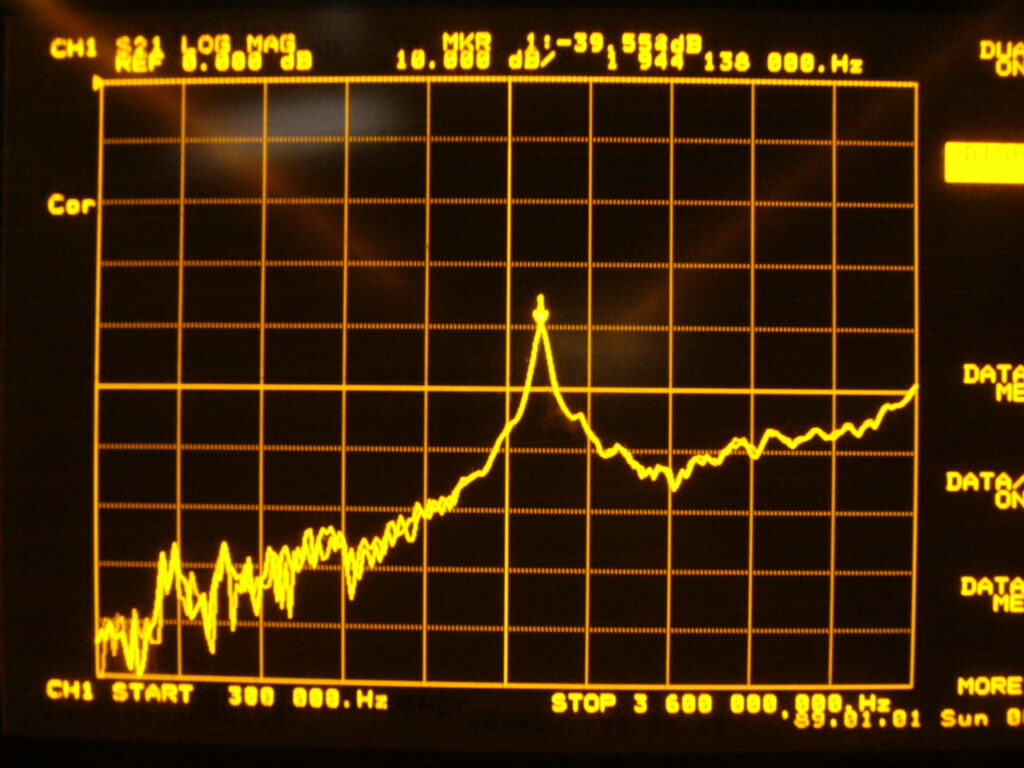
側壁のないサンプル
サンプルに手をかざす,作業台から浮かす,さらにはケーブルや測定器に触ったただけでも,測定値はふらふらと変化する.


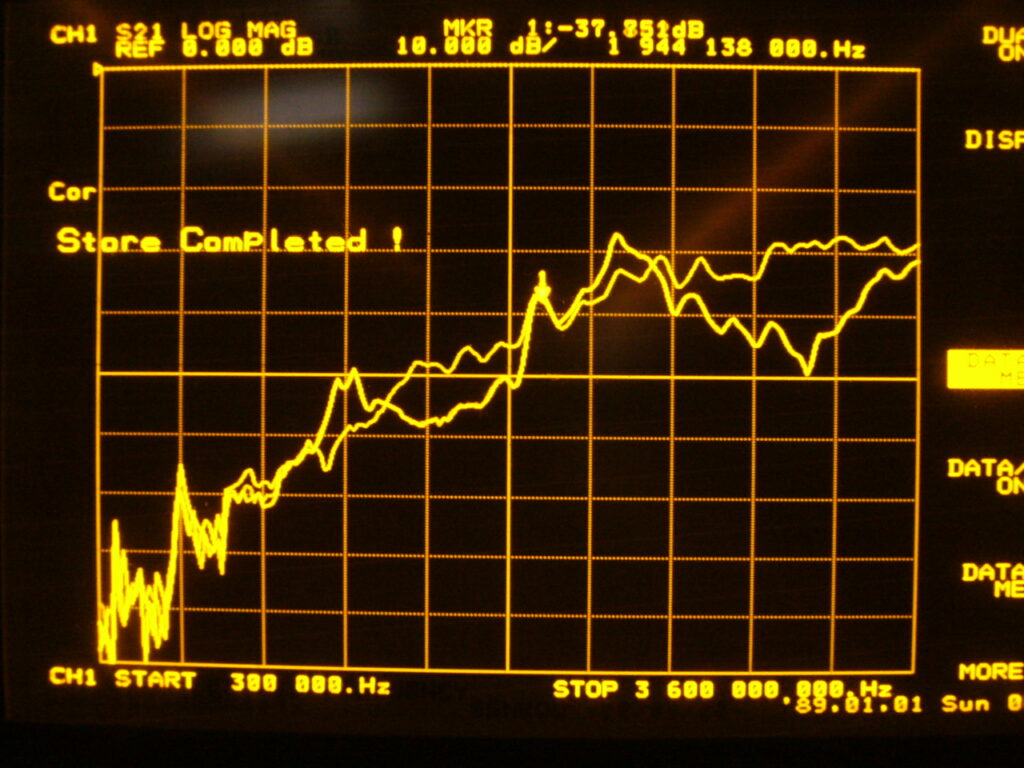
どちらの実験が正しいかは、実験の目的によります. もし、測定環境の不安定さを実証するなら側壁の無いサンプルを 使った実験が正しいといえます. とはいえ、ふわふわと不安定な測定値では結論が出せません.
シミュレーション
この状況はシミュレーションでも再現できます.二つの解析モデルは、それぞれ対応する実験と一致した結果を出します.
側壁に囲まれた空間だけを解析するモデル.
解析時間24秒
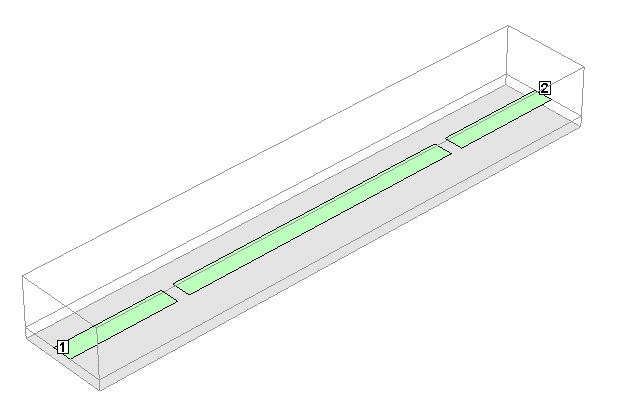
側壁のない基板と,そこから両側にケーブルが伸びたモデル.
解析時間3時間.線路の引き回しや、基板の位置、解析空間の大きさによって結果はころころと変化するはずだが、解析時間が長くそれらを試すことはできない.
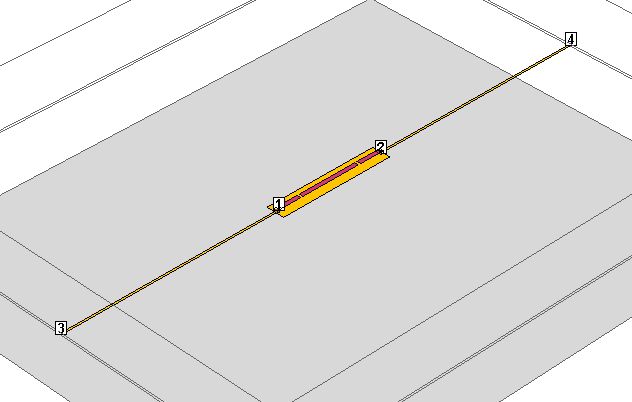
なぜ不安定か?
ソネットのモデルでは、側壁の電位は絶対0Vで、その電位は微動だにしません. 信号はポート1とその側壁との間に接続されますが、A点の電位は変動しても、GND点の電位は決して動きません. 実験の場合は、側壁と天井を導体で取り囲めば、(同軸と同じで)側壁の電位は安定します.天井が開いている場合は、完全ではありませんが、 A点の電位の変動に対して、GND点の電位の変動はずっと小さくてすみます.
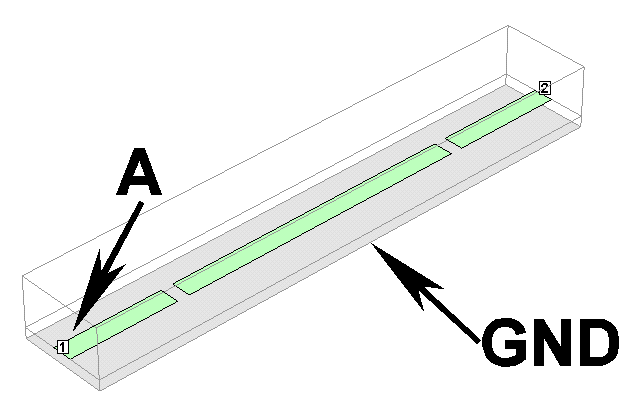
側壁がまったく無い場合は、信号はB点とA点の間に接続されます. B点に対するA点の電位は側壁がある場合と同じですが、 A-B間の信号が空間に漏れ、それがB点の導体に誘導して、 GND点に対するB点の電位が変動します. ソネットのモデルではGND点は側壁ですが、実験の場合は実験室の床や、作業台や、 測定器のシャシや、測定者の体など一定しません. いずれにせよ、A-B間に与えられた信号の一部は B点に誘導し、 それが測定ケーブルの外皮とGND点の間を伝わって、C点やD点に伝播します. その途中で放射も起こりますし、その放射はさらに別の金属に誘導し複雑な現象を引き起こします.
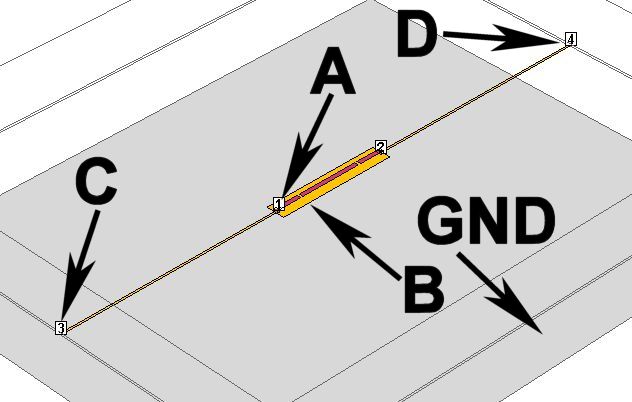
C点,D点は同軸の外皮とGNDとの接続点ですから、 現実には短絡されている場合がほとんどです. しかし、上記のSonnetのモデルでは、短絡せず50Ωポートを設定してあります. これによって、 A-B間に与えた信号のうち、どれくらいの割合が、C点、D点に 漏れるかを知ることができます.
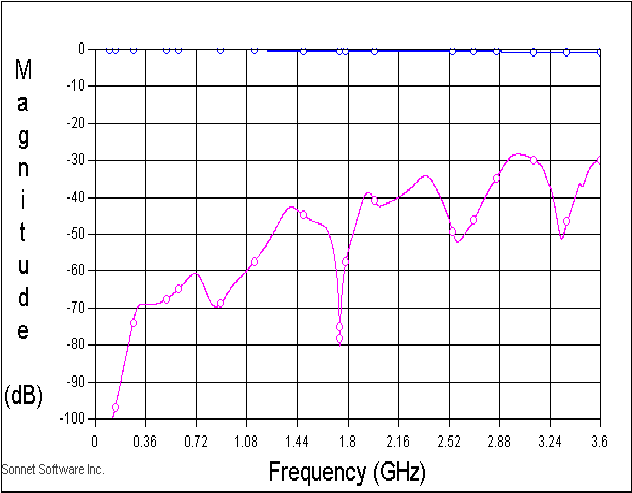
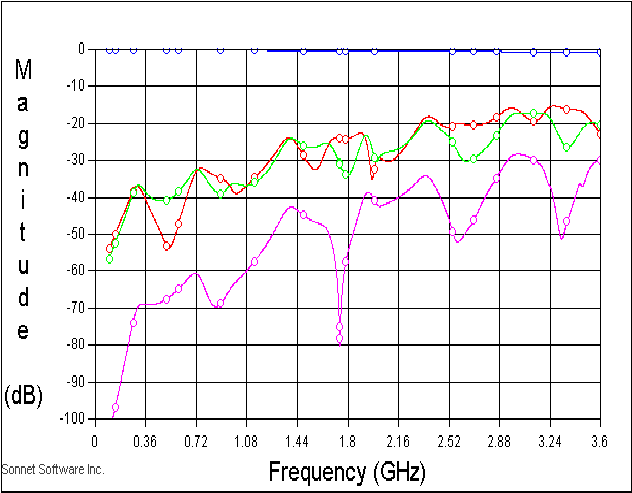
グラフの赤と緑がC点、D点への信号で、 桃色は基板上の直列共振器とキャパシタを通って反対側のSMAコネクタに届く信号です.(測定器に現れる信号) 基板上を伝播する信号の10倍以上の信号が、C点D点へ伝わっていることがわかります . これではいくら基板のパターンやコネクタをいじくり回しても、仕事は終わりそうにありません
それでは?
ここで取り上げた例題のS21は 2GHzの共振点でも-40dBかそこらしかありませんし、 1GHz以下では測定器の限界近い低いレベルです.
市販されているシミュレータの一部はこの問題を解析できないか 非常に大きな誤差を生じるものもあります. ソネットはこのように厳しいレベルの問題を容易に解析できます. 現実の測定には細心の注意が必要です. “シミュレーションの結果は、注意深い測定の結果と一致するのです”.