アンテナの性能を表す利得には様々な定義があります.この記事では送信機から空中に電波が放射されるまでの流れからそれらの様々な利得の定義を説明します.そしてSonnetでそれらの利得を表示する設定.特に全方向に向かって放射されるすべての電波を積分する球面積分についても説明します.またしばしば利得よりも重要な放射効率を求める方法も説明します.
アンテナへの電力の流れ
送信機からアンテナを通して、電波が空中に放射されるまでの電力の流れを下図に整理しました.
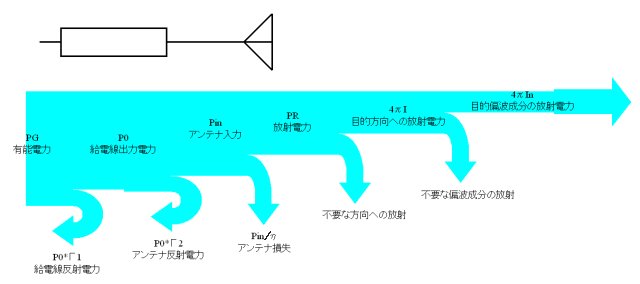
送信機なり、発信機は整合負荷をつないだときに最大の電力を取り出すことができ、その電力を有能電力 \(P_G\)と現します. しかし、実際には完全な整合負荷は得られないので、 発信機と給電線との接続点でエネルギーの一部は反射し、残った\(P_0\)が給電線を通じてアンテナに向かって伝わっていきます.
アンテナと給電線との接続点でも不整合による反射が起こり、給電線を伝わってきた電力\(P_0\)の一部\(P_{in}\)だけがアンテナに入力されます. ここでの不整合については アンテナのSWRとか R.L.として,しばしば不必要なほど厳密に議論されます.
アンテナに入力された電力\(P_{in}\)のさらに一部はアンテナ内部の損失によって熱に変わります.この損失を免れた電力\(P_R\)は無事に空中に放射され電波となります.このアンテナ内部の損失の影響は小型アンテナではしばしば深刻なレベルになるにもかかわらず,忘れられがちです.
多くの場合、空中に放射された電力\(P_R\)は、ある目的の方向への放射電力\(4 \pi l\)のみで評価されます.当然のことながらそれはアンテナからの全放射電力\(P_R\)のうちの一部でしかないので、あくまで等価的なという意味でEIRP(Equivalent Isotropic Radiation Power)と呼ばれます.
上記のEIRPには垂直偏波と水平偏波、あるいは右旋円偏波と左旋円偏波が混在しており、多くの設備ではそれらのうち一つしか受信できません.そこで目的の偏波成分だけの電力を\(4 \pi ln\)と呼んで、上記のEIRP\(=4 \pi l\)と区別することにします.
利得の定義は6種類もある
アンテナの利得は上記の電力の流れのどれを分子にとり、どれを分母にとるかによって6種類もの定義があります.
| 分子→ 分母↓ | \(4 \pi l\) | \(4 \pi ln\) |
|---|---|---|
| \(P_0\) | \(G_w=\frac{4 \pi l}{P_0}\) 動作利得 | \(g_w=\frac{4 \pi ln}{P_0}\) 部分動作利得 |
| \(P_{in}\) | \(G=\frac{4 \pi l}{P_{in}}\) 利得 | \(g=\frac{4 \pi ln}{P_{in}}\) 部分利得=4πln/Pin |
| \(P_R\) | \(G_d=\frac{4 \pi l}{P_R}\) 指向性利得 | \(g_d=\frac{4 \pi ln}{P_R}\)部分指向性利得 |
かつては,これらを区別せず単に”アンテナ利得”と呼んでも誰も気にしませんでした.なぜなら波長の1/4程度以上の大きさのアンテナであれば、内部損失は少なく、整合も容易なので、分母の\(P_0 \approx P_{in} \approx P_R \)はどれも差がなく,どの利得もほとんど同じ値になるからです.しかしアンテナの小型化を進めると整合も難しく,内部損失も大きくなるのでこれらの利得はは有意に異なる値になります.下表はアンテナの大きさ別の重視すべき指標です.
| アンテナの大きさ | 整合 | 内部損失 | 指向性 | 設計のポイントと重要な指標 |
| \(\le \lambda / 10 \) | 帯域が狭く困難 | 損失が大きい | ブロード | 効率 \(\eta=\frac{P_R}{P_{in}} \) |
| \( \lambda /5 \sim \lambda /2 \) | 容易 | 小さい | ブロード | 実装構造など |
| \( \lambda \le \) | 容易 | 小さい | 鋭い | 指向性 \(G_d\) |
sonnetで扱うことの多い小型アンテナではアンテナに入力されたエネルギー\(P_{in}\)のうち、空中に放射されるエネルギー\(P_R\)の割合、つまり放射効率\(\eta\)が重要です.
sonnetのpatvuでの実例
上記の様々な利得をSonnetのpatvuを使って表示してみます. 一例として”パッチアンテナの設計例“から”有限なグランド導体上の一点給電円偏波パッチアンテナ“の利得を調べてみます.Sonnetを使ってアンテナの解析をなさる場合は,→この文書に従ってください.
まず、分子が \(4 \pi l\) の場合
| 利得 | 設定 [Graph]-[Graph Options…]-[Normalization] | 結果 |
|---|---|---|
| 動作利得 | 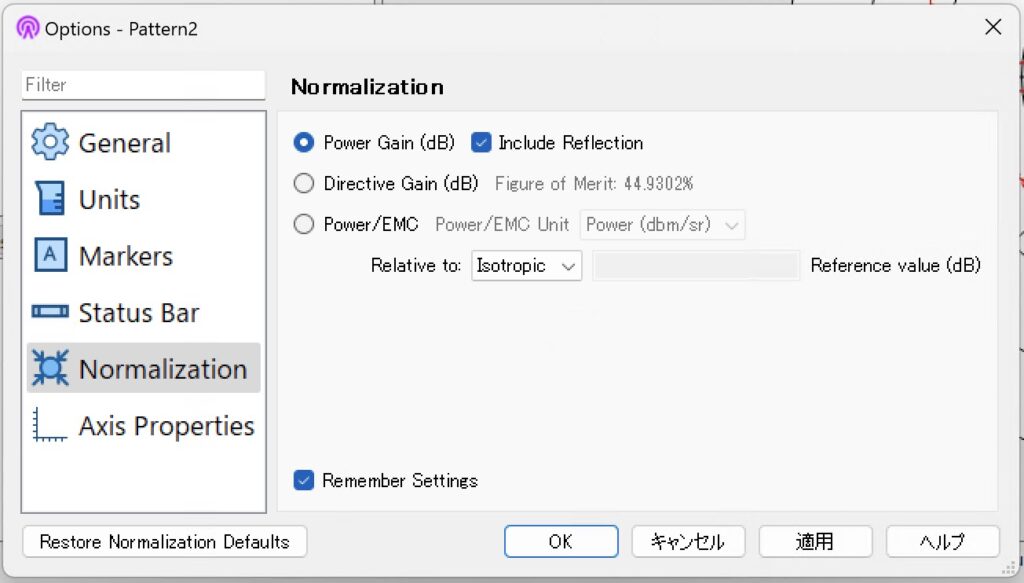 | 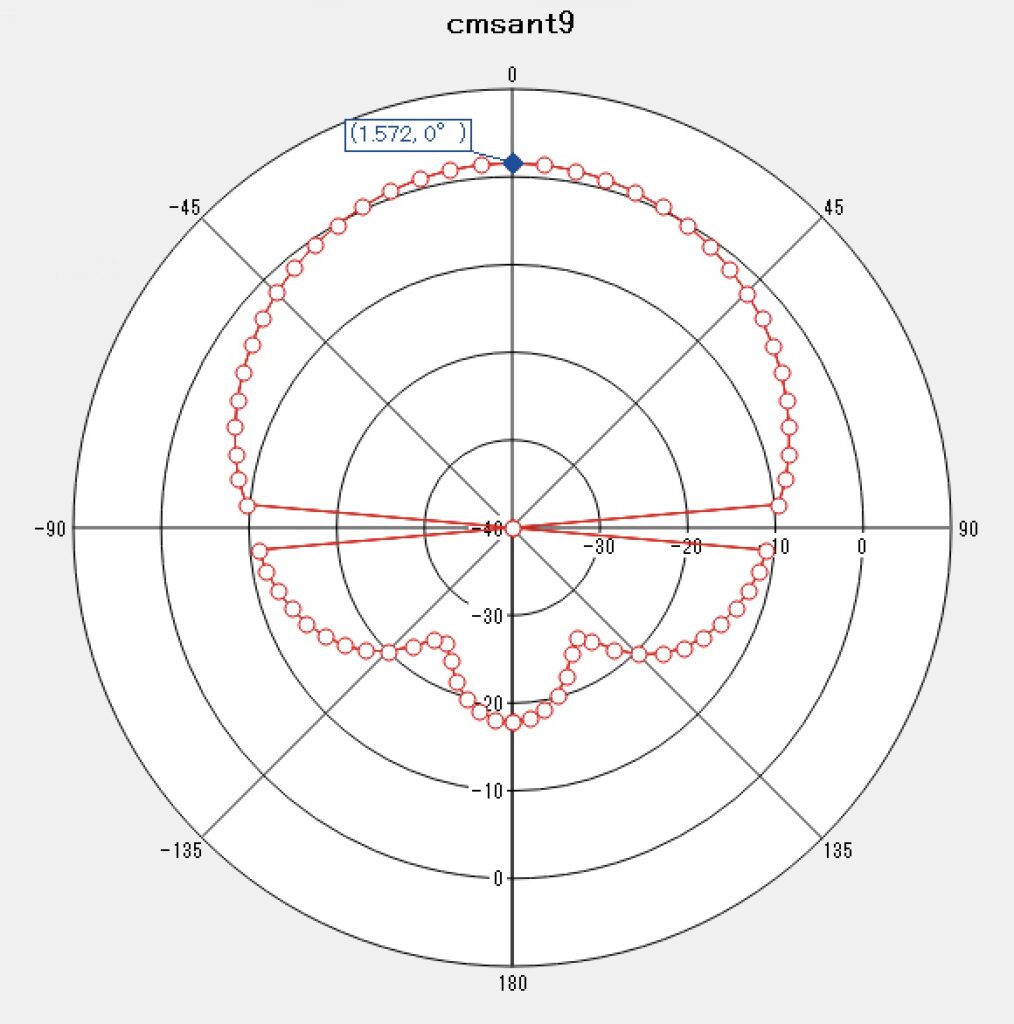 \(G_w= 1.572\mathrm{dB}\) |
| 利得 | 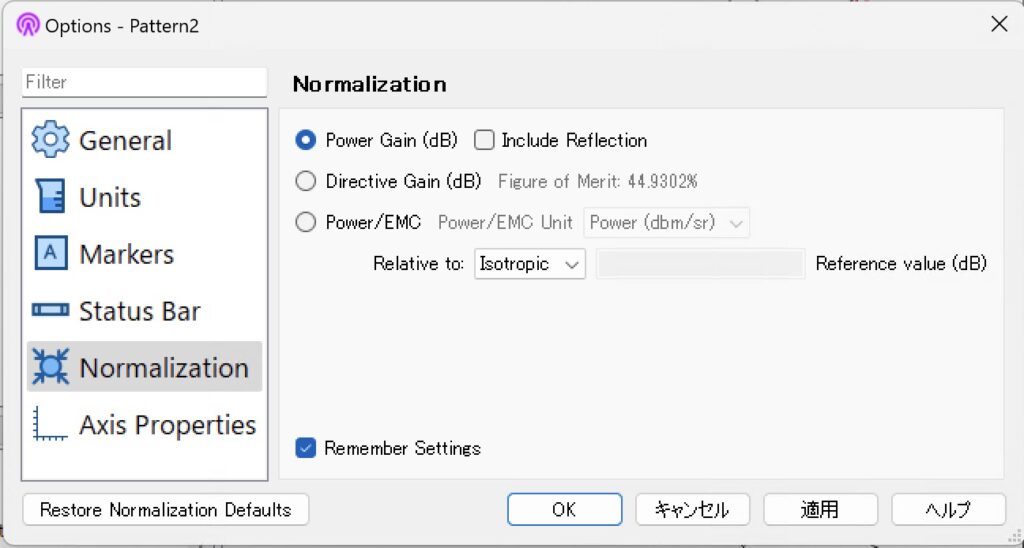 | 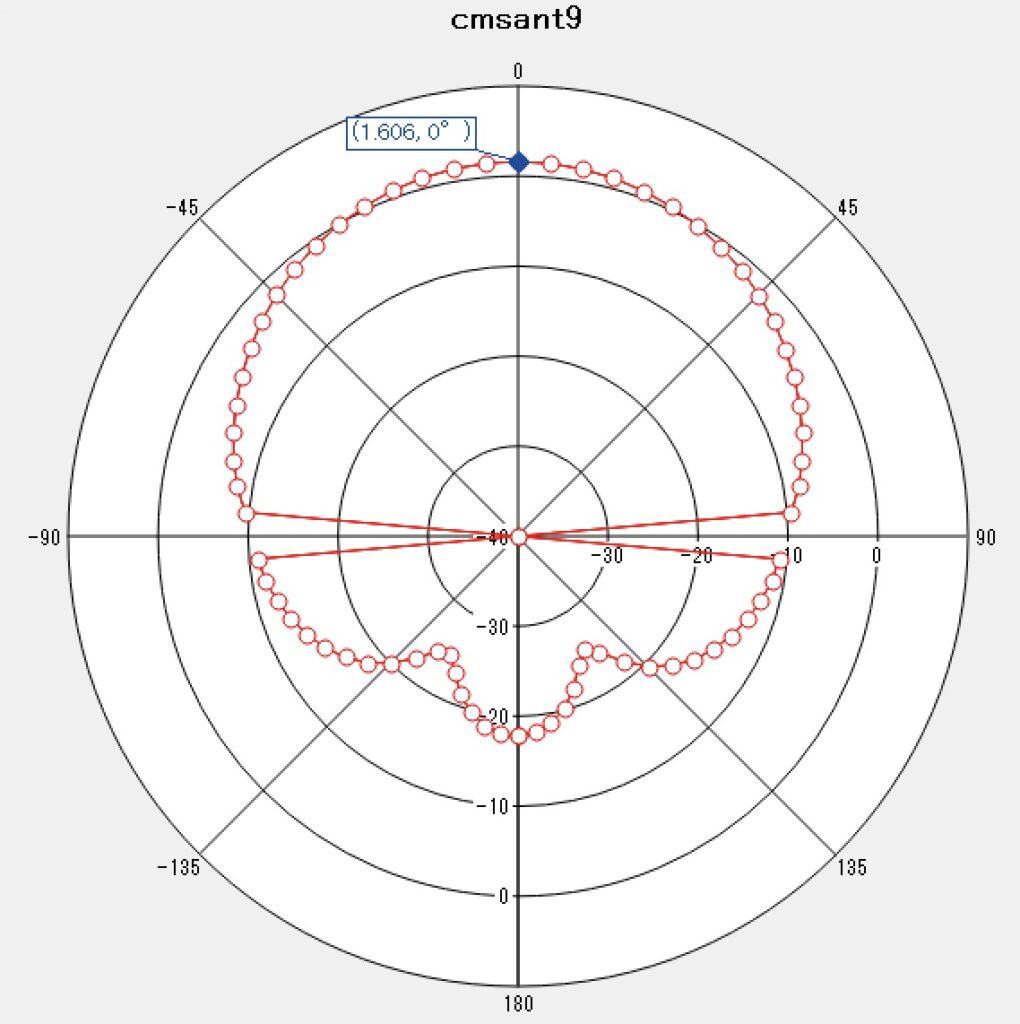 \(G= 1.606\mathrm{dB}\) |
| 指向性利得 | 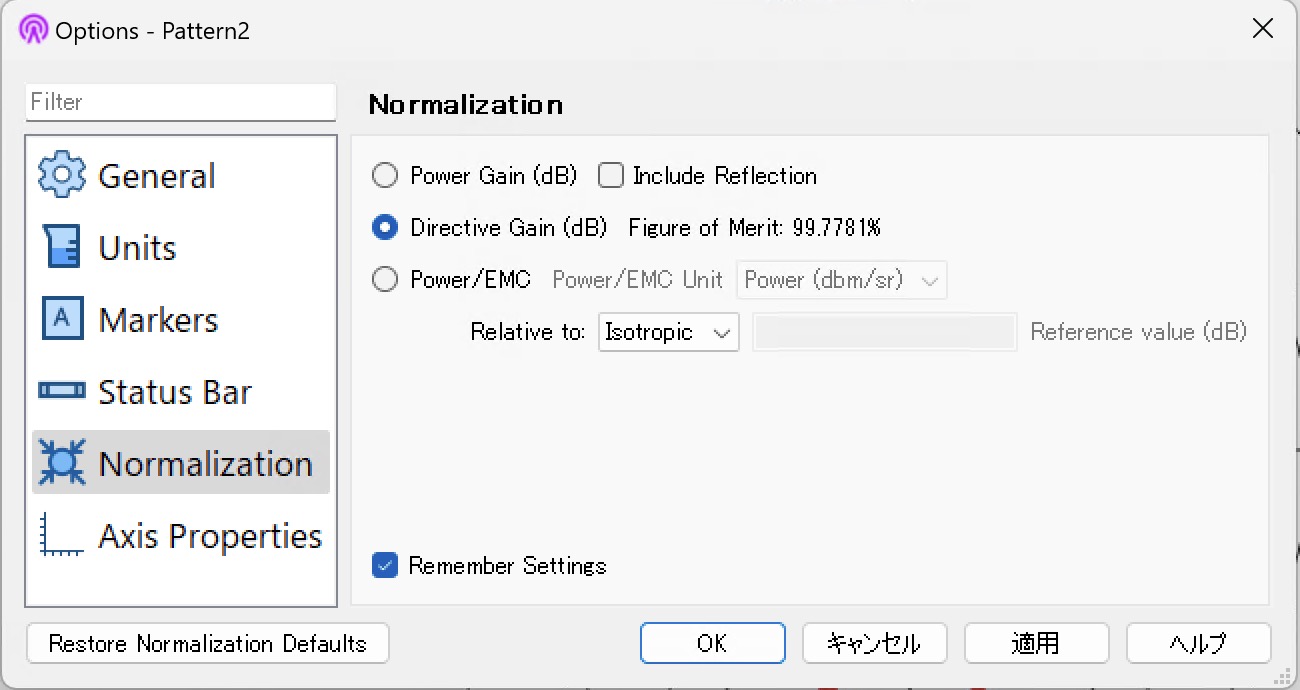 | 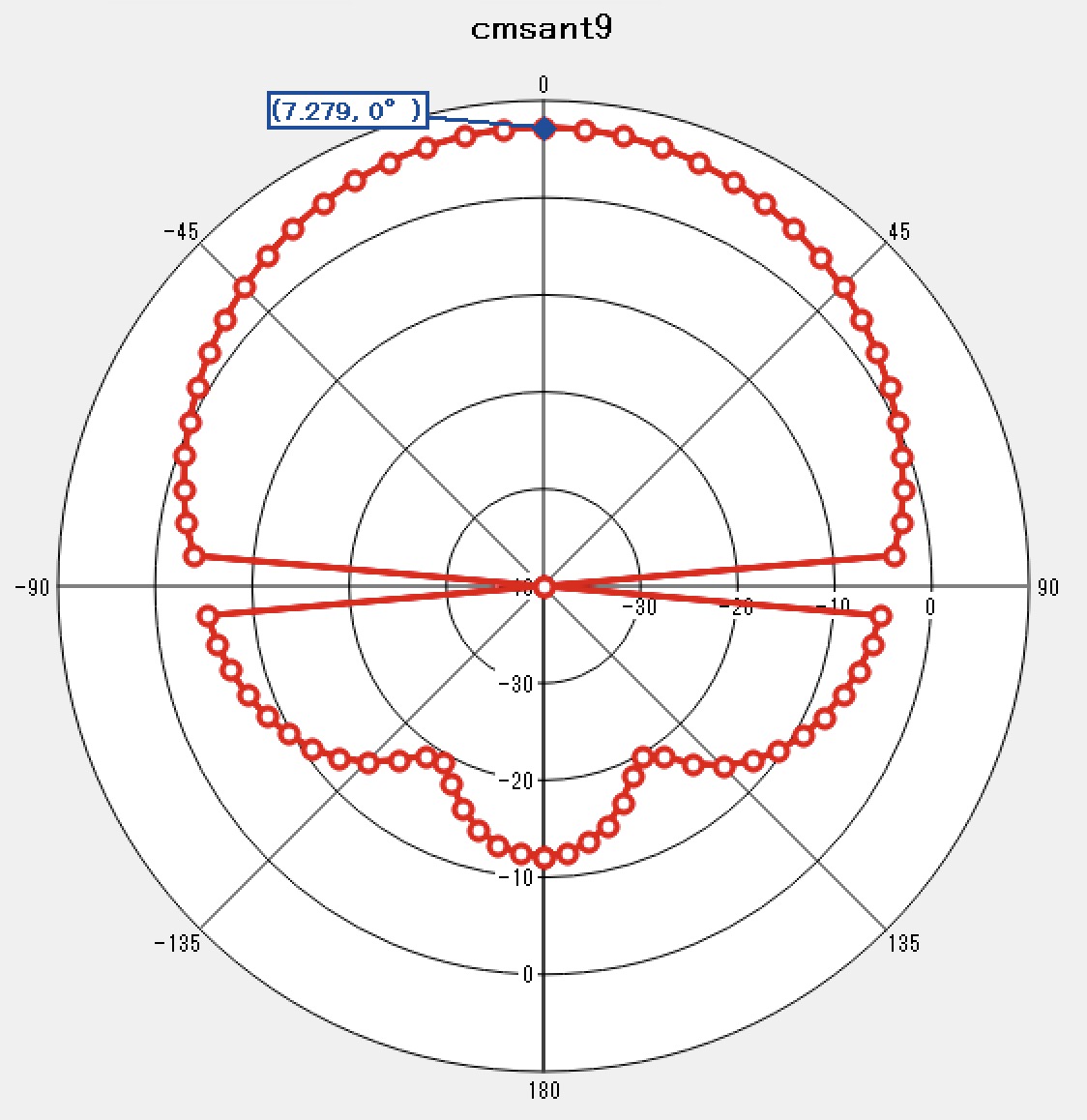 \(G_d= 7.279\mathrm{dB}\) |
次に、分子が \(4 \pi ln\) の場合は patvuのメニューで[Graph]-[Manage Curves…]でダイアログを開き、目的の偏波成分を選択します.
こうしてSonnetはアンテナの全ての利得を算出することができます.
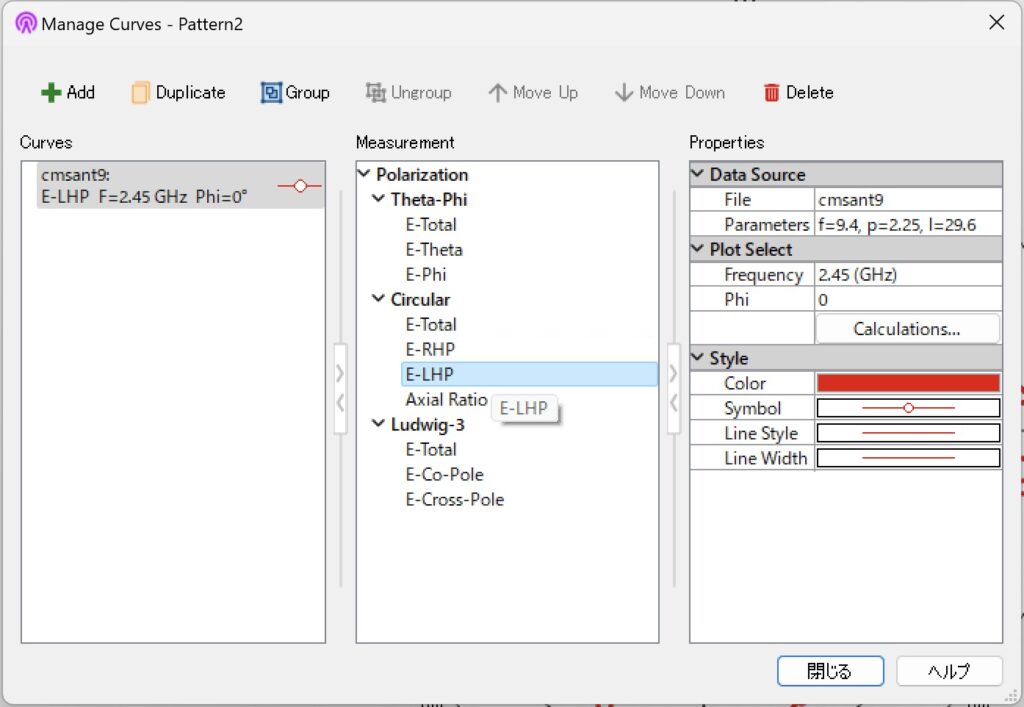
全放射電力\(P_R\)の算出に必要な球面積分について
patvuのメニュー[Graph]-[Graph Options…]-[Normalization]でDirective Gainの項目に、Figure of Merit(FOM)が表示されます.これは指向性利得\(G_d\)を算出するときの分母\(P_R\)(全放射電力)をどれほど正確に計算したかを示しています.
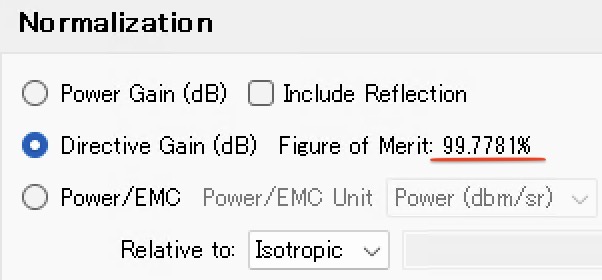
全放射電力\(P_R\)を算出するためにはアンテナをとりまく球面を通過する放射電力を、その球面の全面積に渡って積分しなくてはなりません.数式で書けば
\(P_R=\int_{-\pi/2}^{\pi/2} \int_{-\pi}^{\pi} P d \theta d \phi\)
これは全球面の積分です.しかし理想的なグランド導体を持つパッチアンテナのようにboxのbottom metalが導体の場合は、下半球への放射は存在し得ないので
\(P_R=\int_{-\pi/2}^{\pi/2} \int_{-\pi/2}^{\pi/2} P d \theta d \phi\)
上半球だけの積分になります.
この積分の積分範囲と数値積分の刻み幅はユーザーが指定しなくてはなりません. patvuのメニューで [Graph]-[Calculations…]でCalculation Setup ダイアログを開き、[Angles]タブを選びます.これが、上記の積分の積分範囲と刻み幅です.
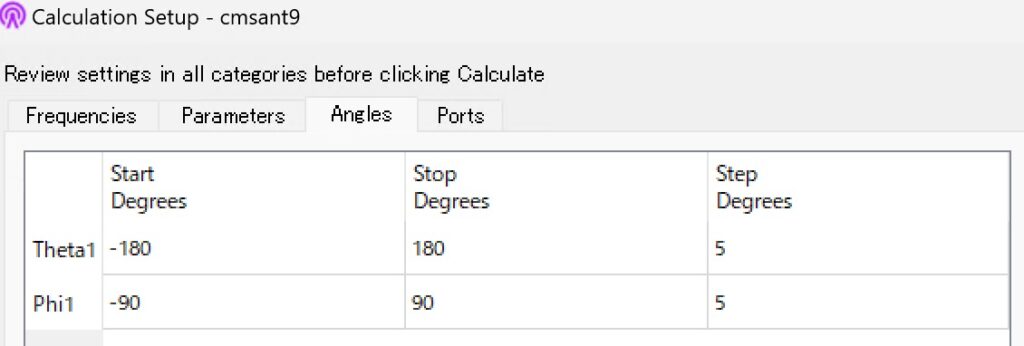
積分範囲が正しく全球面や上半球をカバーしていれば、方向性利得\(G_d\)を表示したときにFOMは100%に近い値をさします. 刻み幅が荒すぎると90%や80%になるかも知れません.よくある間違いは、積分範囲の指定を誤って、同じ面を二回積分してしまうことです.この場合のFOMは200%近い値になり、方向性利得\(G_d\)には大きな誤差を含んでしまいます.
放射効率\(\eta\)を求めるには
球面積分から求めた全放射電力\(P_R\)と入力電力\(P_{in}\)との比で求める方法
放射効率ηは、
\(\eta = \frac{P_R}{P_{in}} = \frac{G}{G_d} =\frac{g}{g_d}\)
です.上記の例では \(G=
1.606\mathrm{dB}\), \(G_d=
7.279\mathrm{dB}\) なので、\(\eta=G-G_d=-5.673\mathrm{dB}=27\%\) です. このアンテナは1/2波長四方のパッチアンテナで,基板厚が波長に対して\(\frac{1}{80}\)という薄さです.それゆえ帯域は狭く,効率も低いアンテナです.\(\eta\)が50%にも満たないので、\(P_R\)の積分精度FOMは90%程度で十分です.
一方,\(\lambda / 2\)ダイポールアンテナでは効率\(\eta\)では99%を超えるので\(P_R\)から効率\(\eta\)を求めるなら\(P_R\)の計算精度も3,4桁必要なのです.FOMでいえば99.9〜99.99%程度必要です.
Qファクターから求める方法
放射効率\(\eta\)を求めるために球面積分を使わない方法です. この方法ではSonnetのpatvu(遠方界放射解析ポストプロセッサ)オプションは不要で,無料のSonnetLiteでできます.
- 求めるアンテナの解析モデルをコピーしてください.オリジナルのモデルをlossed_model,コピーしたモデルをlossless_modelと呼ぶことにします.
- lossless_modelに含まれる全ての導体をlosslessに指定してください.
- lossless_modelに含まれる全ての誘電体の損失を0に指定してください.
- lossed_modelとlossless_modelをそれぞれ解析してグラフに描きます.
- ふたつのグラフが重なるなら、放射効率\(\eta\)はとても良いはずで、これ以上追求するのは時間の無駄です.
- ふたつのグラフがズレていたなら,2つのQの比が放射効率\(\eta\)です.Qを求めるために下記の2つの方法があります.
方法1 インピーダンスかアドミタンスの傾斜からQを抽出する方法
“共振回路のQファクター“に,Qを抽出するユーザー定義関数,理論背景,そしてアンテナ放射効率を抽出する実例の動画があります.
方法2 完全に整合したときの3dB帯域幅から求める方法
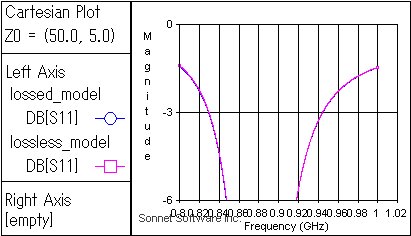
lossed_modelとlossless_modelがそれぞれ、求める周波数で完全に共役整合になるようにemgraphのメニュー[Graph]-[Terminations]で終端条件を調整します. 少なくとも中心周波数でS11<-30dBを実現してください. このとき、lossless_modelとlossed_modelで終端条件が違ってもかまいません.
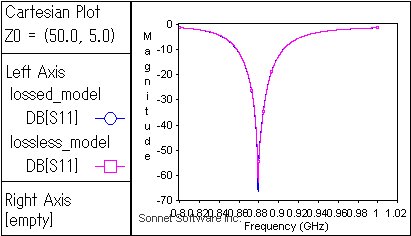
lossed_modelとlossless_modelの-3dB帯域幅をグラフから読み取ります. グラフの目盛りや、解析周波数分解能を工夫する必要があるかもしれません.この例では lossed_modelは114.8MHz,lossless_modelは114.4MHz でした.
放射効率は lossless_modelの3dB帯域幅 / lossed_modelの3dB帯域幅 =99.6%です.