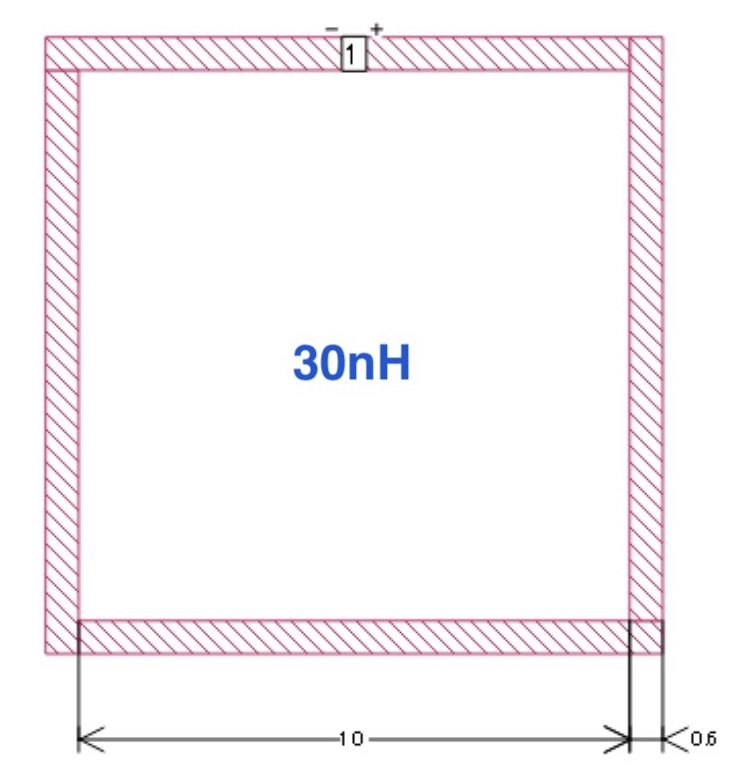
波長よりずっと小さなコイル状のパターンを sonnetで解析する場合の基本をまとめました.周囲にコイルの直径程度の空間を確保すること,丸いコイルは四角に置き換えること.解析周波数を極端に低くあるいは高くしなこと,損失が重要な場合は無料版では難しいことなどを解説します.
周囲の余裕
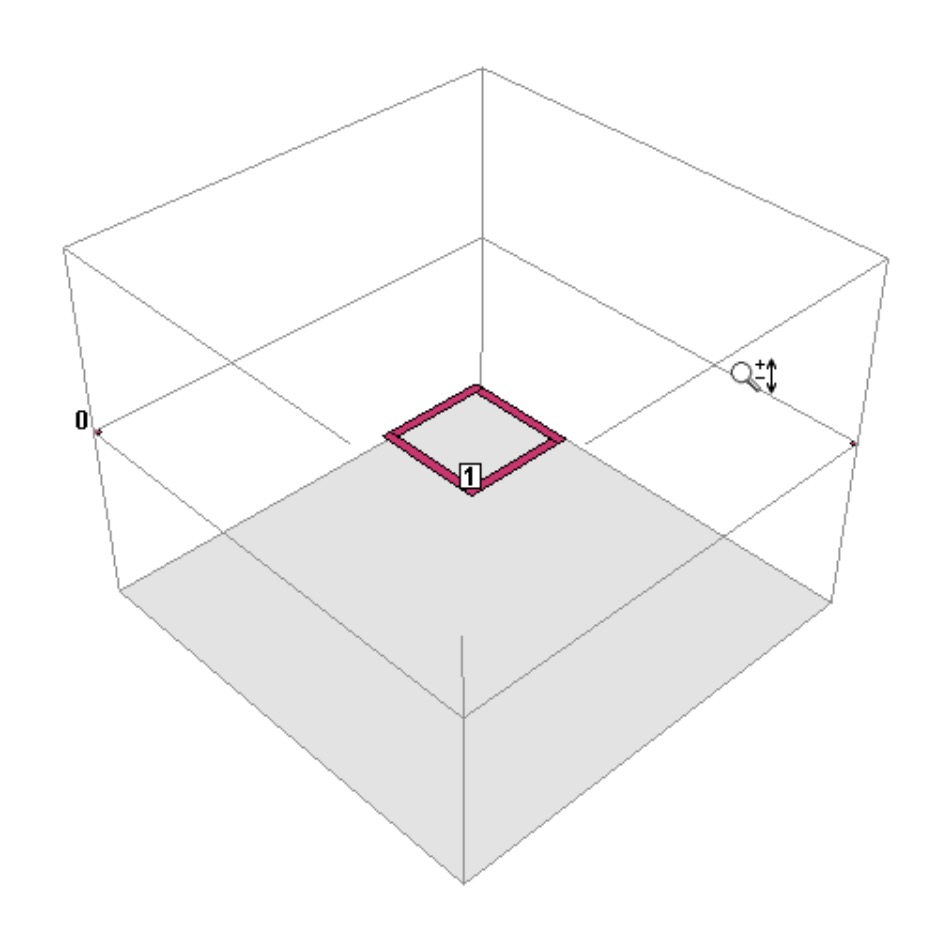
四方と上下に同程度の空間をもたせる.少なくともコイルの直径と同程度でなければならない.3D表示で[View][Option…]でZ-scale=1に設定して右図のようにほぼ立方体の形になってなければ何か間違っている.
厳密さが必要な場合は,top metal,bottom metalの影響が無視できるレベルになるまでコイルの直径の2倍,4倍と変化させて結果の収束を確認する.
Boxのtop metal,Bottom metalをfree spaceに設定するのはよくある誤解.ここでのfree spaceとは\(377\Omega\)シート抵抗という意味で,波長の短い電磁波に対しては自由空間として振る舞うが,コイル周辺の磁界に対しては抵抗膜でしかない.
free spaceとLosslessの解析結果を比べて有意な差があるなら解析空間が狭い.解析空間を広げると急激に結果は収束するはず.しかし解析負荷も急激に重くなる.コイルの直径の4倍,8倍とかでも満足できないならそもそも何かが間違っている.(たとえば波長よりずっと小さなコイル状という前提が崩れるほど高い周波数で解析しているとか)

円形コイル
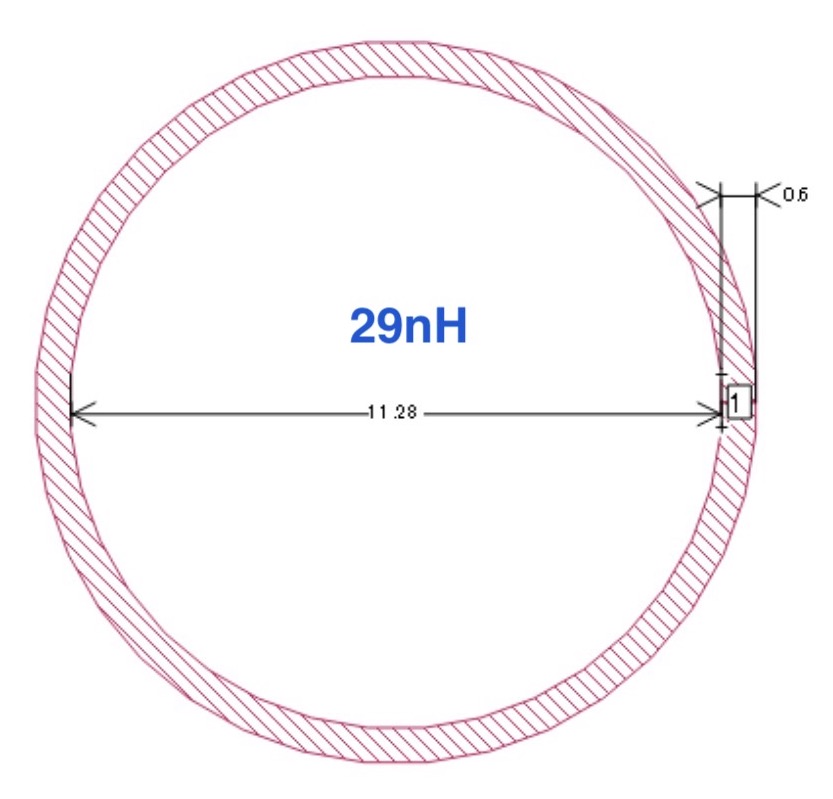
どうしても円形で解析する場合はセルサイズを線路幅の半分未満に設定する.
斜めの線がガタガタでも,電流は右図のように斜めに流れるので結果への影響は少ないが,セルサイズを線路幅程度まで大きくすると斜めの線路が切断され非常に大きな誤差を生じる.
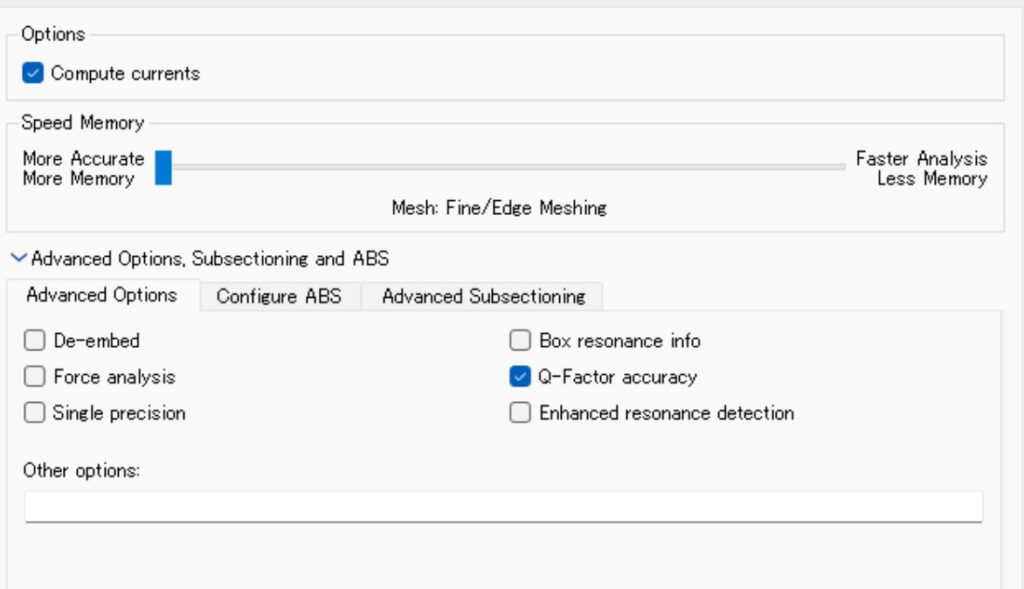
解析設定と周波数範囲
[circuit][settings…]のメニューで[EM options]ページのAdvanced Optionで[De-embed]のチェックは外して良い.これによりポート周辺の微小な浮遊容量が解析結果に含まれるがインダクタンスの解析では影響は非常に小さい.
コイルのモデルでは導体面積が小さいのでSpeed Memoryスライドバーはほとんど効果がない.
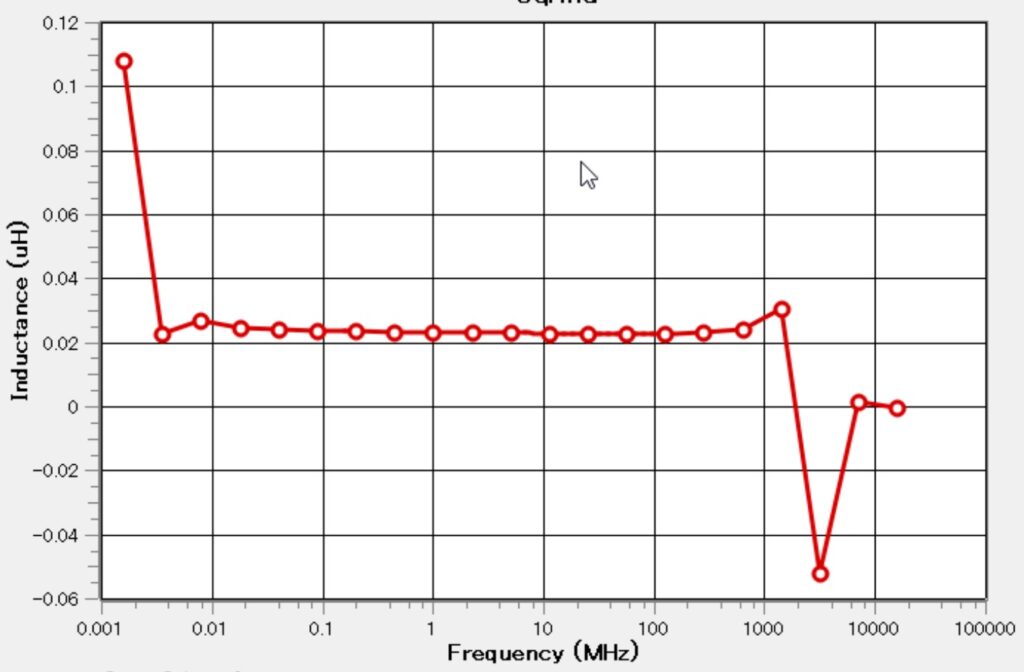
低い周波数領域を含む3桁程度の広い周波数領域を指数関数的に解析し結果が安定している領域で評価すること.ABSは不要.

右図のグラフは理解のために8桁の周波数領域の解析結果を対数グラフで示している.0.002MHz以下ではSonnetが大きな解析誤差を出している.2000MHz付近に自己共振があり,3000MHzではさらに解析空間自体が共振している.0.03Mhzから300Mhzの間であればどこで解析してもインダクタンスはほぼ同じ値になる.この領域で解析すること.
この例では特に\(0.159\mathrm{(MHz)}\)がおすすめの周波数.\(0.159\mathrm{(MHz)}\)では\(L\mathrm{(\mu H)}=Im(Z)\mathrm{(\Omega)}\)なので,インダクタンスとインピーダンスの変換が直感的にできる.
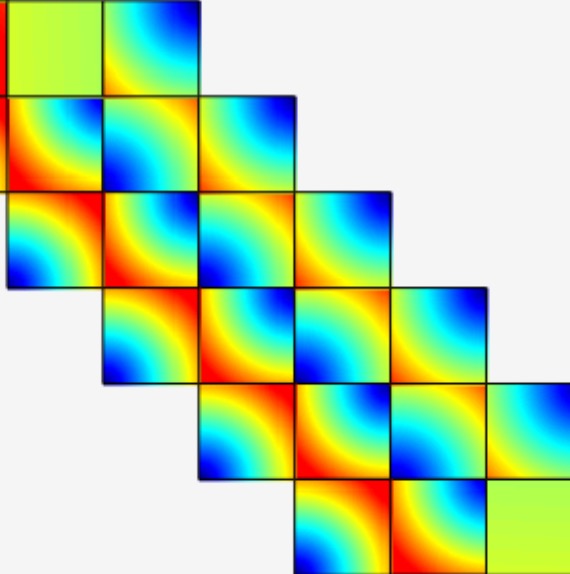
導体損失が重要な場合は細かなセル
導体損失が重要な場合は(円形であれ正方形であれ)セルサイズを導体幅の1/3以下に設定し,電流が導体の縁に沿って集中する様子を再現する.
無料版では解析規模の制限に掛かる可能性がある.

[circuit][settings…]のメニューで[EM options]ページのAdvanced Optionで[Q-Factor accuracy]にもチェックを入れる.これによりABSの内部の収束判定に損失項を含めるようになる.
Speed Memoryスライドバーは右端にしてはならない.右端では導体端部のサブセクションを省略するので電流集中を再現できない.

上位の製品版ではConformal meshを指定することで解析時間を大幅に短縮できる.Conformal meshは電流が導体の縁に沿って流れるなら正しい結果を得られる.これは導体幅が波長より遥かに小さいならと言い換えることもできる.
セルサイズが導体幅の1/3程度ではConformal meshの解析時間は返って遅くなる可能性がある.