解析時間が遅いと感じたときに,解析の内部の工程を大まかに知っておくと効果的な対処ができます.この文書では解析の内部の工程の概要を説明し,実際の解析時に各工程が消費するCPU時間やメモリ消費を調べる方法,そして各工程ごとの対処方法を説明します.
sonnetの解析の工程とボトルネック
sonnetの内部では matrix fill, matrix solveの2つの工程を条件を変えながらsweepしています.各工程ごとに解析時間を短縮する手段は違うので,どの工程がボトルネックかによって対処も異なります.
解析工程
| 工程 | ボトルネックになる問題 | 対処 |
| matrix fill 連立方程式を作ること | アンテナ conformal meshを多用した問題 | セル数を2のN乗にする 層の厚みをむやみに増やさない |
| matrix solve 連立方程式を解くこと | ほとんどすべての問題 | セルを大きくする←重要 |
| de-embedding ポート校正 | 部品を使っている問題 グランド付きコプレナ線路 | [Insert]-[compornent]..による部品を使わない 幅の広い導体をポート面に接続しない |
| sweep 条件を変えて繰り返すこと | 複数のパラメータをパラメータスイープしたり最適化する場合 | 複数のパラメータを同時にスイープしない 周波数スイープではABSを使う |
ボトルネックを調べるには
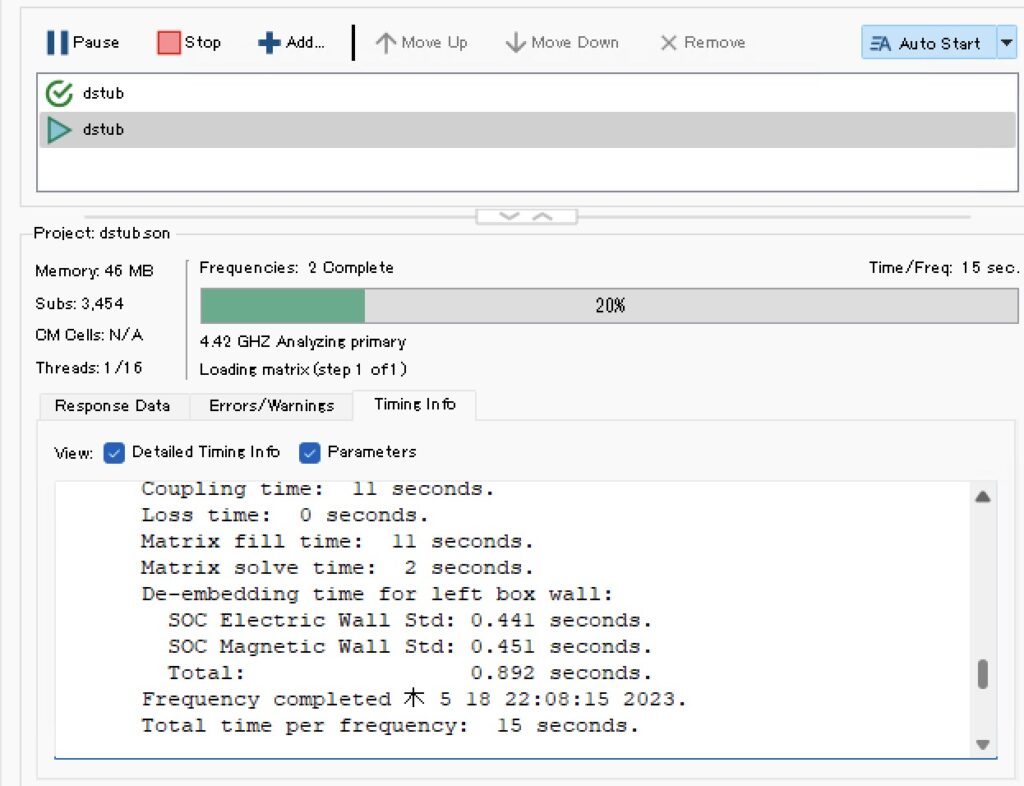
解析後に[Job Queues]タブを開き,調べたいプロジェクトの解析Queueを選んで,[Timeing Info]タブをクリックすると,解析logの中から時間やメモリに関する情報だけが表示されます.
この例では
Matrix fill : 11sec Matix Solve : 2sec De-embedding : 0.892sec
などの情報からmatrix fillがボトルネックだとわかります.
matrix fill
matrix fillは連立方程式を作る工程です.これは行列の要素をひとつひとつ埋めていく作業なので matriix fillと呼ばれます.
解析空間の大きさ
行列の各要素は与えられた解析空間に存在しうるすべての電磁界のパターンが各要素に与える影響を計算して行列の要素を埋めてゆきます.空間が大きいほど存在しうる電磁界のパターンも増えるのでmatrix fillの計算時間が増えます.解析空間は適正な大きさにしてください.
- マイクロストリップ回路では基板上の空間は基板厚さのせいぜい5倍から10倍,回路から壁までの距離は基板厚さと同程度か2倍
- アンテナでは空間層の厚さは1/4波長,アンテナの周囲の壁までの距離は1波長
- 波長より非常に小さなコイルやトランスでは,上下の空間層や周囲の壁までの距離はコイルの直径と同程度かせいぜい2倍以内
解析空間の狭さが解析結果に及ぼす影響を確認するには,まず上記の適切な解析空間で解析し,次に周囲の空間を2倍にして解析し結果にどれほどの差が生じるかを確認してください.
Number of Cells
解析空間中の平面を何個に区切るかが”Number of Cells”です.これはアンテナの場合に大きな数字になる場合が多く全体のボトルネックになる可能性が高いです.[Circuit Settings]で”circuit settings”ウィンドウを開き,[Box]ページの”Num.cells:”が”Number of Cells”です.
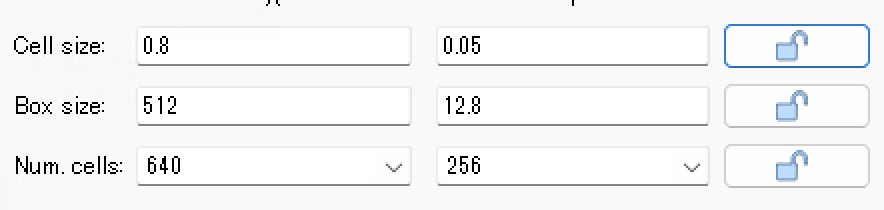
number of cellsの値は2のN乗が好ましいです. 512, 1024, 2048, 4096などです.この数字にできない場合は ディスプレイの分解能に使われる数字を思い出してください.768, 800, 900, 1200, 1280, 1440, 1600, 2560 など,これらはすべて コンピュータにとってキリの良い扱いやすい数字で number of cellsに適しています.
最悪な数字は 1031とか4099とか..これらは大きな素数です.67とかの小さな素数なら気にすることはありませんが,4096と4099ではびっくりするほど計算時間に差がでます.
マイクロストリップ回路では”number of cells”は小さいので,この基準を忘れてしまっても構いません.アンテナの場合はこの程度の大きさにすることはよくあります.
原理
sonnetの内部では電磁界のパターンが各要素に与える影響を計算するために,使えるときはFFT(Fast Fourier Transform)を使います.これはとても早い計算方法ですが,”number of cells”が2のN乗の場合しか使えません.sonnetはFFTが使えない場合は別の手段を使いますが,それでも計算時間は”number of cells”に依存します.”number of cells”が 2のN乗+3のM乗+5のL乗+……というふうに小さな素数で表現できるなら良い数字です.
matrix solve
sonnetのCellは大胆に大きく
Cellの大きさは次のように考えて決めてください
- 1/8波長より小さく
- 線路や導体片がなくなったり切れたりしない限り大きく
- 波長より小さいガタガタは気にしない,円弧は直方体に置き換える
見た目の印象でリアルな形状を再現するようにCellの大きさを決めると間違いなく細かすぎます.大きなCellを指定する心理的な障壁がSonnetを使う上で最も難しい点かもしれません.
Cellの大きさが解析結果に及ぼす影響を確認するには,まず上記の適切なCellの大きさで解析し,次に”Numbwer of Cells”を2倍に(つまりCellの大きさを半分に)して解析し結果にどれほどの差が生じるかを確認してください.
speed/memoryスライドバー
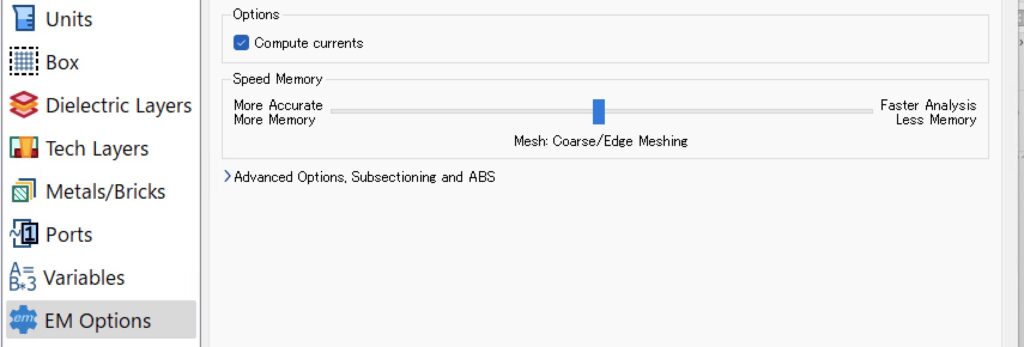
sonnetは波長と導体形状を考慮して重要な部分はCellをそのまま,そうでない部分は多くのCellをまとめて大きなSubsectionを作ります.
[Circuit Settings]で”circuit settings”ウィンドウを開き,[EM Options]ページの”Speed Memory”というスライドバーでこのSubsectionの大きさを指定できます.おすすめは中央の位置です.
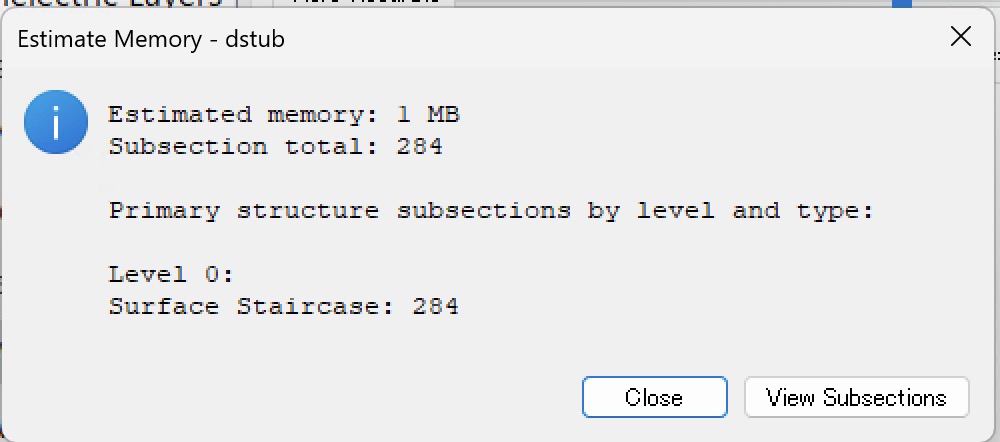
下のほうの[Estimate Memory]というボタンをクリックすると,sonnetは指定したスライドバーの条件でSubsectionを作ってみて,何個のSubsectionがメモリをいくつ使うかが表示されます.ここでさらに[View Subsections]ボタンをクリックするとSubsectionの様子をビジュアルに見ることができます.
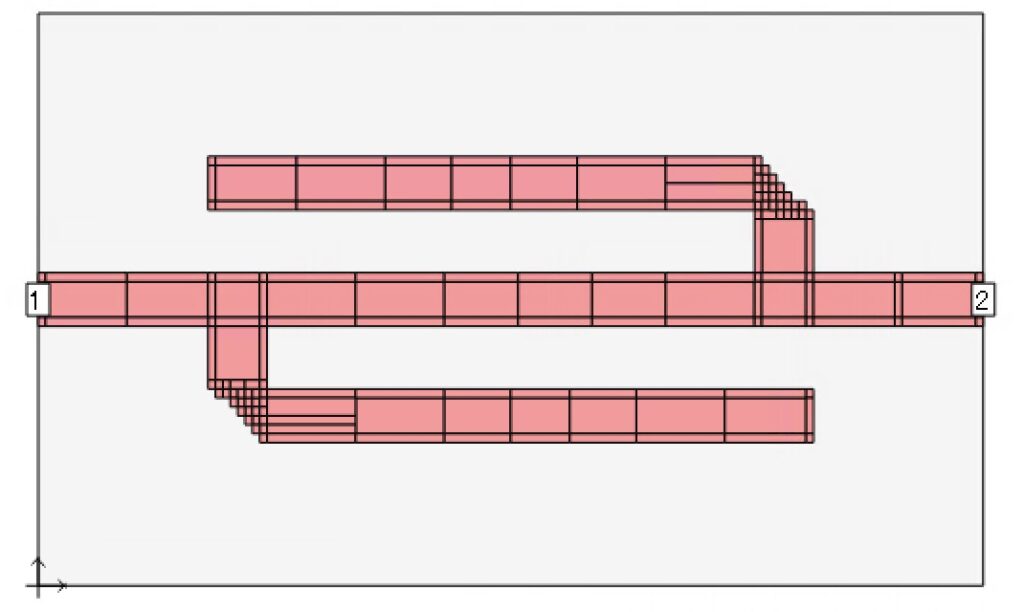
これはSubsectionの一例です.高周波電流は導体の縁に集中するので導体の縁に細長い細かいSubsectionが配置されています.
N元連立方程式を解く計算時間はNの3乗
N個の未知数をもったN元連立方程式を解く計算時間はNの3乗に比例することがわかっています.Nが2倍になれば計算時間は8倍になるので未知数の数Nが一定以上になると現実には解けなくなります.これはsonnetに限らず多くの科学技術計算に共通の課題なので長年涙ぐましい努力が続けられていますが,未知数の数Nを減らすことと以上に効果のある方法はありません.
sonnetは導体パターンを多くの長方形の導体片に区切って,その各導体片に流れる電流を未知数として連立方程式を解きます.sonnetではその導体片をSubsectionと呼んでいます.Subsectionは複数のCellの集合です.Cellは解析空間全体を”Number of Cells”の数で区切った要素です.
したがってCellを大きくすることが計算時間を短縮する基本になります.
Cellの対角線に沿ったSubsectionを使う”Diagonal mesh”や,電流が導体の縁に平行に流れると仮定して曲線や斜めの導体を大胆に大きな部分にまとめる”Conformal mesh”の機能が,上位グレードの製品では実装されています.それらは長年の涙ぐましい努力の成果ですが必ず弱点がありますし,あいかわらずCellを大きくすることは最も重要です.ご自身でHELPを読んで理解した上で使ってください.
De-embeddingを早くするには
部品
[Insert]-[compornent]..による部品を使うと部品の数に比例してDe-embeddingの時間が増えます.特に無料のSonnetLiteではこの方法による部品の種類も数も厳しく制限されていますし,精度に関しても褒められたものではありませんから使わないほうがよいでしょう.入門書の“2.6 部品と関数 -バイアスティー”では,解析が早く,精度にも優れた部品のモデルを紹介していますから,そちらの方法の方をお薦めします.
グランド付きコプレナ線路
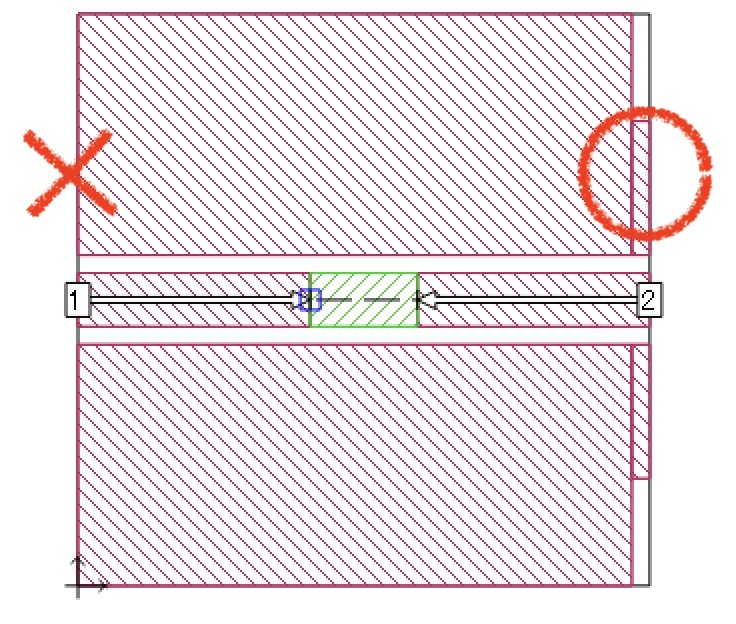
グランド付きコプレナ線路のグランド導体の幅を細くしてください.
例えば信号導体の幅wならグランド導体の幅は2w程度で十分なはずです.モデル全体に広いグランド導体があったとしてもポートに接続する部分だけはグランド導体の幅を狭くしてください.
右図の左側のポートは悪い例,右側のポートは良い例です.
原理
マイクロ波の測定の前に測定器のポートに標準器を接続して測定することで測定器のポートを校正するのと同じように,sonnetは解析に先立ってすべてのポートを校正しようとします.ポートに寄生している寄生素子を論理的に取り除くという意味でDe-embeddingと呼びます.
部品が接続する接続点もポートなので部品が増えるとDe-embeddingの回数が増えます.
測定器の標準器は規格化された同軸コネクタですが,Sonnetが使う標準器はそれぞれのポートの形状に応じてSonnet自身が生成します.具体的には長さの異なる複数の線路を標準器として使います.その複数の長さの異なる線路それぞれにたいして,本当の解析と同じように”Matrix fill, Matrix solve, sweep”を行います.幅の広い導体がポート面に接続されていると,その太い導体を延長した複数の線路には多くの未知数が含まれるため,本来のモデルの解析よりも時間がかかることすらあります.
高周波電磁界シミュレータでは,この厳密なDe-embeddingを全く行わない製品が多いなかで,Sonnetは厳密なDe-embeddingを行うので解析のダイナミックレンジが広く,厳密な部品モデルを使った場合には優れた精度が得られます.しかし厳密な部品モデルの入手元は限られますし解析負荷も重いです.またDe-embeddingをするための構造の制限が強いられることもあります.
そのため特にアンテナ問題ではDe-embeddingしないほうが便利です.
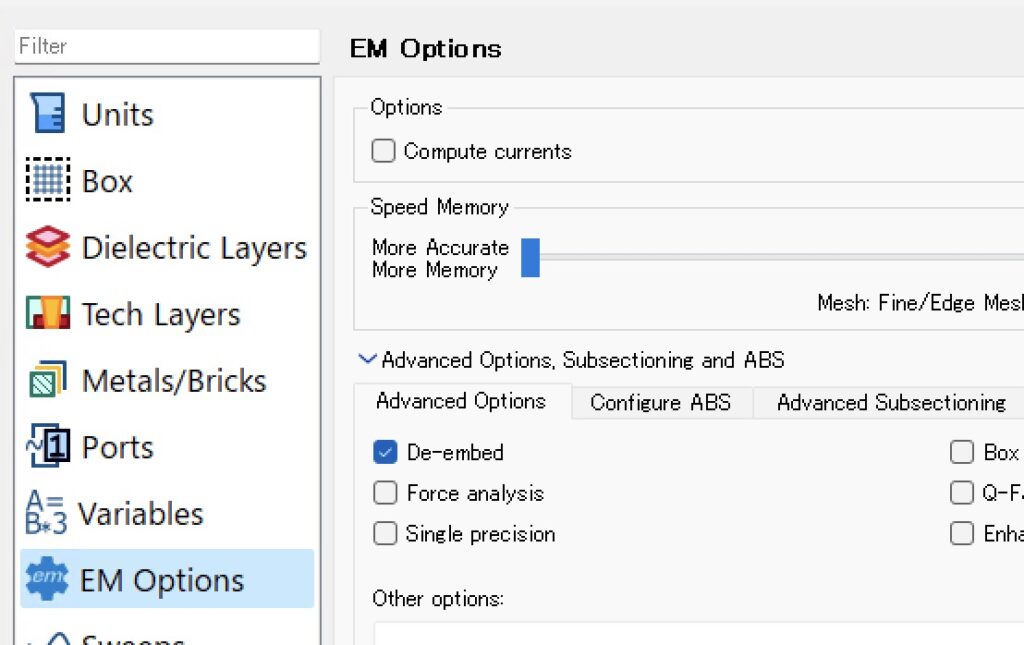
[Circuit Settings]で”circuit settings”ウィンドウを開き,[EM Options]ページで[Advanced Options. Subsectioning and ABS]をクリックし,高度なオプションを表示します.そのなかの[De-embedding]のチェックを外すとDe-embedingをしなくなります.
sweepを早くするには
Adaptive Sweep
matrix fillやmatrix solveに比べてsweepの計算時間は予想しやすいです.しかしsonnetのAdaptive Sweepには注意が必要です.
Adaptive Sweepは最後にsweepする
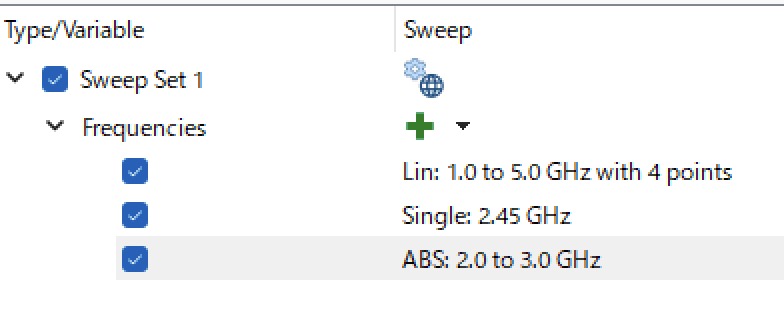
[Circuit Settings]で”circuit settings”ウィンドウを開き,[Sweeps]ページでSweepを指定します.
右図のようにAdaptive Sweepは,他のSweepが終わった最後に置いてください.そうすればAdaptive Sweepはすでに終わった解析結果から最適な仕事をします.さもなくばAdaptive Sweepと他のsweepの結果に微妙な矛盾が起こってしまいます.
Adaptive Sweepは高い周波数の限界がある
メニューで[Circuit]-[Estimate Box Resonances]を選んでください.
右図では ”45.89GHz TE Mode 0,1,1″ と表示されています.この数字がAdaptive Sweepの周波数の限界です.この周波数以上ではAdaptive Sweep以外のsweepを使ってください.

パラメータsweepでは一つずつsweepしましょう
sonnetでは周波数sweepだけでなく,モデルの寸法や様々な解析条件を変数に指定してパラメータsweepすることができます.無料版では一つのパラメータしかsweepできませんが,上位グレードの製品ではsweepするパラメータの数の制限もありません.
例えば第一のパラメータを5通り変化させ,第2のパラメータを5通り変化させ,第3のパラメータを5通り変化させると解析時間は 5x5x5=125倍です.同時にsweepするパラメータが増えると解析時間は急激に増えます.まして最適化では一つのパラメータを”何回試すか?”の回数も決まっていないのでいつまで立っても終わらない場合が多いです.
メモリー使用量
次の理由で近年メモリー使用量はあまり重要ではなくなりました.
- 無料版Sonnet LiteでMatrix fillが使用するメモリー使用量の制限が(こっそり)解除された
- Matrix solveの計算時間は未知数の数Nの3乗に比例するが,メモリー使用量はNの2乗にしか比例しない
- PCに実装されるメモリが非常に多くなった
それゆえ2023年の時点で,解析規模の現実的な制限は未知数の3乗で増大する計算量で決まります.


