sonnetの誤差は要素数に対して単調に変化します.それゆえ極端に要素数を増やさなくても,少ない要素数を変化させるだけで収束値の予測が可能です.この文書は米国ソネット社の Error Convergence in Sonnetの日本語訳 です.
単調な誤差収束の重要性
収束分析とは、問題を基本セルサイズに設定しEM解析を行い,次にセルサイズを半分にし再解析します。それぞれの解析の後、解が漸近的に正しい値に収束しているかどうかが比較されます。
収束分析には2つの目的があります。
- 電磁波解析ソフトの収束が遅いのか、間違った答えに収束してしまうのか、発散してしまうのかを調べることができます。
- 粗いグリッドで解析を早く設計を進め,最後にセルを細かくして望ましい精度に「収束」しているかどうかを判断することができます。
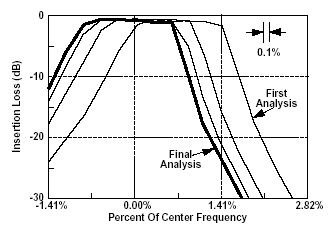
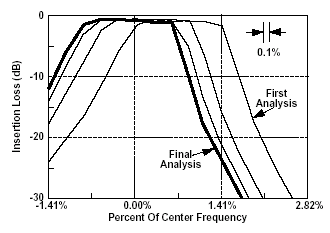
Sonnetの収束性は、多数の回路で検証されています。グラフは、Sonnetの収束テストの一例で、セルサイズによって結果を収束している様子を示しています.
セルサイズの変化に従って誤差が単調に収束することは、シールドドメイン・モーメント法、特にSonnetの特長の一つです。どのような結果であっても、セルサイズを細かくあるいは荒くすることで結果の収束性を判断することが可能です。Sonnetが確実に単調な誤差収束を示すという知識を持っていれば、シミュレーションの品質を確信することができます。
訳注
- sonnetの誤差は単調に収束しますが,解析手法によってはセル(グリッド)の大きさに対して誤差が振動するもあります.そのような場合は結果の収束を確認するのは容易でなく,時間のかかる細かいグリッドを使わざるを得ません.
- sonnetの場合セルサイズの各辺を半分にすると未知数は4倍,計算量は64倍になるので,セルサイズを細かくするよりも荒くして収束を調べたほうが現実的です.計算量については多くの文献(例えばこの3.2.3)があり,殆どのシミュレータに共通の性質です.
- このトピックはこの動画“20161123 基礎講座TH1B ゼロから始める電磁界シミュレーション”,あるいは“数値計算シミュレータ常識のウソ”にも説明してあります.