
| アンテナ解析モデルを作る場合に注意すべきことをまとめてあります. |
適用範囲
この解説は、ダイポールアンテナ、パッチアンテナ、逆Fアンテナなどの単一の周波数で動作するアンテナとそのアレイに適用される. UWBに代表される広帯域通信向けのアンテナでは、より複雑な要素が含まれるので、ここでの解説をそのまま適用できない.. また、13MHz RFIDに代表される近傍界アンテナ(または磁気結合アンテナ)はそもそも動作原理が異なる.
アンテナの等価回路
ここで取り上げるアンテナは、その共振周波数の近傍では、Qの低い 共振回路と等価とみなすことができる. そして、その共振回路に関して、 共振周波数において外部回路が完全に整合しているとすれば、 放射効率や帯域幅を容易に定義できる.
| 並列共振回路 | 直列共振回路 | |
|---|---|---|
| 回路図 | 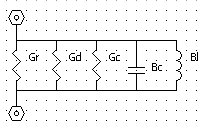
|

|
| 等価損失 |
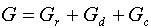
|
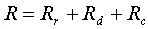
|
| 無負荷Q |
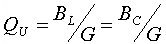
|
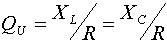
|
| 3dB帯域幅 | 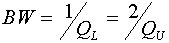
|
|
| 放射効率 |
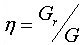
|
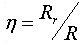
|
なお、ここに
- Gr,Rrはそれぞれ、空間への放射により失われるエネルギーを
- Gd,Rdはそれぞれ、アンテナ近傍の誘電体損失により失われるエネルギーを
- Gc,Rcはそれぞれ、アンテナ近傍の導体損失により失われるエネルギーを
小型アンテナの放射効率と帯域幅
アンテナでは一般的に Gr>>Gd,Gc 、 Rr>>Rd,Rc でアンテナ放射効率 は殆ど1である.ところが、 アンテナの機械的な外形を極端に制限した小型アンテナでは、 Gr,Rrが小さくなり、 それにともなって 放射効率と帯域幅が低下する. 放射効率はアンテナ全体のパフォーマンスを低下させるし、 帯域幅の低下は整合回路の歩留まりを低下させる.
放射効率と帯域幅の評価法
測定であれシミュレーションであれ、 帯域幅は単にアンテナ端子からアンテナを見たインピーダンスを観測すれば容易に知ることができる. ところが放射効率の算出には放射に起因するエネルギー損失 Gr,Rrを分離して知る必要があるので、実際に空間に放射するエネルギーを測定しなくてはならない. ところが、空間に放射するエネルギーを精度良く測定することは容易でない. これに関してはシミュレーションを使って" アンテナの利得"に記載のGwまたはGで評価するとはるかに容易に精度良く評価できる.これらのパラメータには放射効率だけでなく不整合による損失や、不要な方向への放射も含まれているが、幸いにシミュレーションでは完全な整合を実現することは難しくないし、放射損失が問題視されるような小型アンテナでは指向性はブロードになるので問題にならない.
等価回路定数算出の一例
一例として このパッチアンテナの等価回路の定数を調べてみる.
周波数分解能を上げるため複数の周波数スイープを組み合わせて解析し、 結果をグラフにして必要なデータを読み取る
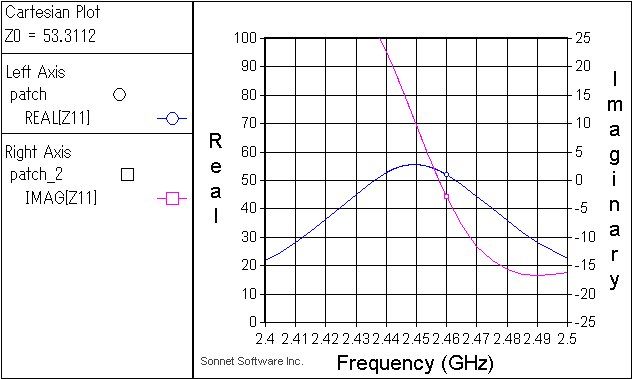
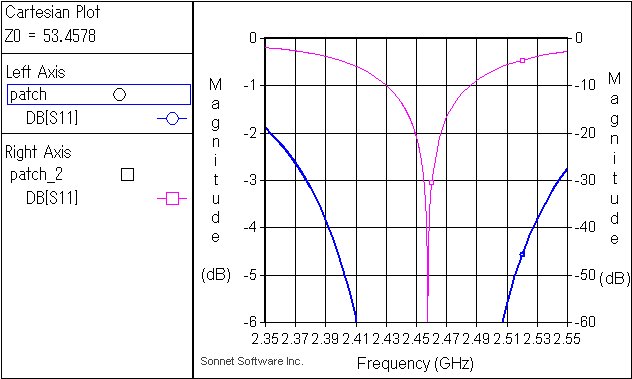
| Im(Z)=0になる周波数 | 2.4575GHz |
| そのときのRe(Z) | 53.4578Ω |
| Zo=Re(Z)としたとき S(11)が-3dBになる周波数 | 2.3776-2.5441GHz |
この共振系の無負荷Qは 2 * 2.4575 / (2.5441-2.3776)= 29.5
並列等価回路
等価コンダクタンス G = 1 / R = 1 / 53.4578 = 18.706mS
等価キャパシタンス C = G * Q / ω
C = 29.5 / 53.4578 / 2 / π / 2.4575G = 35.739pF
等価インダクタンス L = 1 / G / Q / ω
L = 53.4578 / 29.5 / 2 / π / 2.4575G = 0.11736nH
直列等価回路
等価レジスタンス R = 53.4578Ω
等価インダクタンス L = R * Q / ω
L = 53.4578 * 29.5 / 2 / π / 2.4575G = 102.13nH
C = 1 / 53.4578 / 29.5 / 2 / π / 2.4575G = 0.041067pF
検証
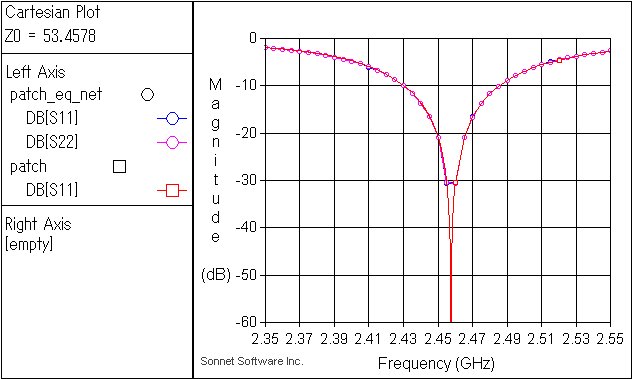 二つの等価回路ともdB(S)で評価すると、もとのアンテナの特性と完全に一致する.
二つの等価回路ともdB(S)で評価すると、もとのアンテナの特性と完全に一致する.
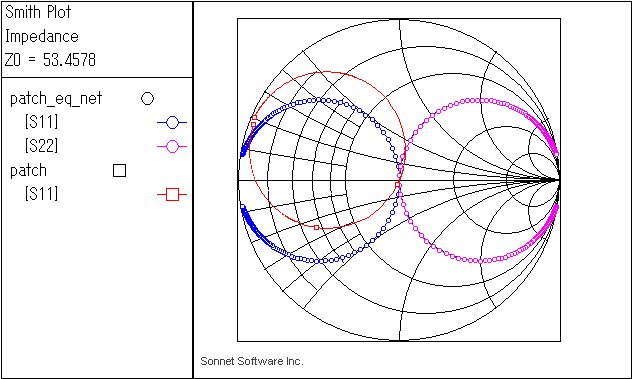 しかしスミスチャートで見ると一致しない.このアンテナの場合、並列等価回路が比較的良く一致するが、それでも位相は完全には、一致しない.これらの差異は給電構造に起因するが、アンテナのファンダメンタルな動作には影響しないので、どの等価回路を使ってもかまわない.
しかしスミスチャートで見ると一致しない.このアンテナの場合、並列等価回路が比較的良く一致するが、それでも位相は完全には、一致しない.これらの差異は給電構造に起因するが、アンテナのファンダメンタルな動作には影響しないので、どの等価回路を使ってもかまわない.
